86-Q3: Resistivity, Using a Wheatstone Bridge

Time 1$\frac{1}{2}$ hr.

Apparatus

Metre bridge & jockey; resistance wire (length $\approx$ $1\text{m}$, resistance $\approx 2 \Omega$ but not less); metre rule; resistors ($0.5\Omega, 1\Omega, 2\times 2\Omega, 5\Omega, 10\Omega, 20\Omega$); $1.5\text{V}$ cell; galvanometer; 4 connecting leads (3 long, 1 short); 1 sheet graph paper; micrometer.

The aim of this experiment is to determine the electrical resistivity of the wire provided. Proceed as follows:

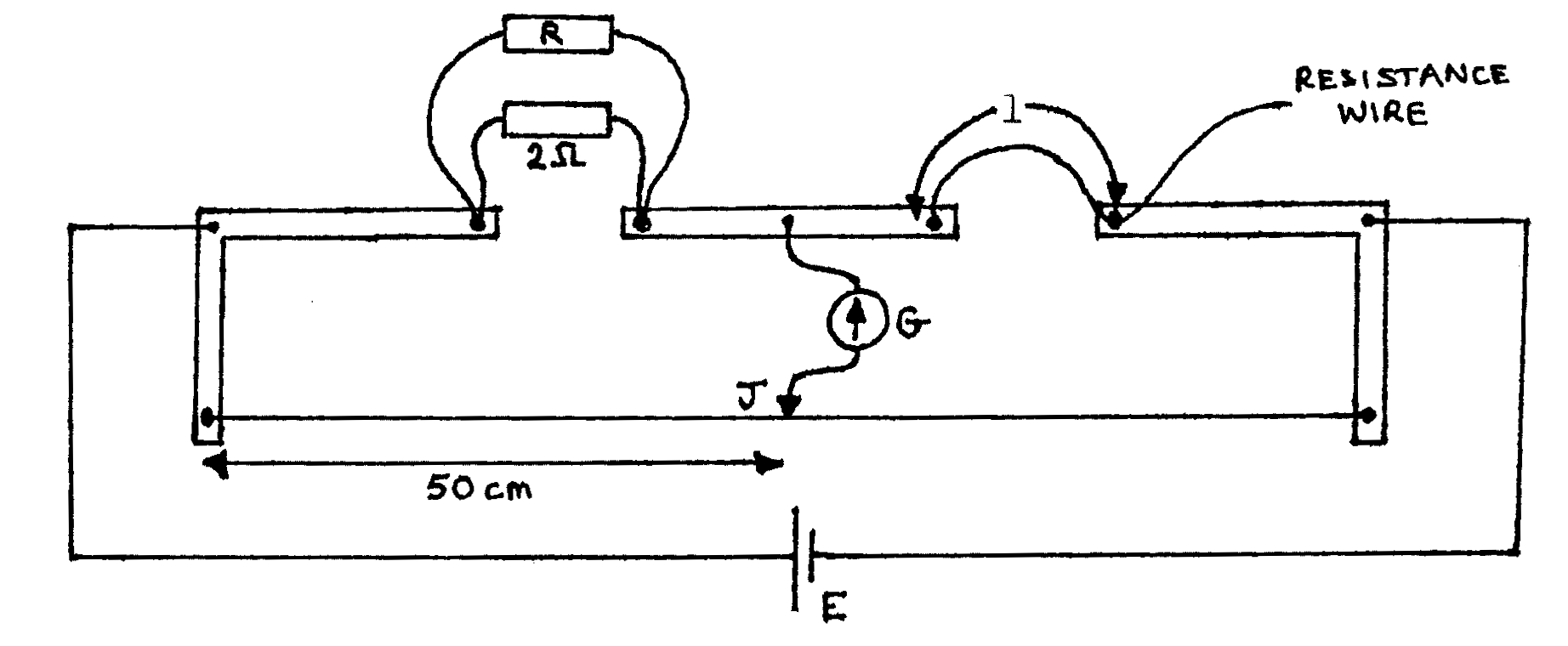
1. Set up a slide-wire metre bridge as illustrated below where E is a cell, G is a Galvanometer, length $l$ of the resistance wire is connected across the right-hand gap of the bridge, and the jockey or slider J is placed at the $50\text{cm}$ mark.
2. With R $= 20 \Omega$, find the value of length $l$ for which the galvanometer gives zero deflection when the slider is tapped onto the $50\text{cm}$ mark as shown below. (2 marks)
3. Repeat the procedure in (b) for values of R equal to $10\Omega, 5\Omega, 2\Omega, 1 \Omega, \text{ and } 0.5 \Omega$. (8 marks)

1. Calculate and tabulate the values of $\frac{1}{R} \text{ and } \frac{1}{l}$ for the values of $R$ equal to $20\Omega, 10\Omega, 5\Omega, 2\Omega, 1\Omega, \text{ and } 0.5\Omega$ obtained in (b) and (c) above. (7 marks)

2. By means of the micrometer screw gauge provided, measure the diameter of the resistance wire, and hence calculate its average diameter $d$. (5 marks)

3. Plot a graph of $\frac{1}{R} \text{ vs. } \frac{1}{l}$ (whose values are recorded in i above) and determine the gradient. (12, 5 marks)

4. Determine the resistivity $\rho$ of the resistance wire given that:

   $$\frac{1}{R} = \frac{A}{\rho} \frac{1}{l} - \frac{1}{2}$$

   Where $A$ is the cross-sectional area of the resistance wire. (4, 7 marks)